È stata pubblicata ieri 30 marzo la soluzione del problema I giardini di marzo. Ogni mese la prestigiosa rivista scientifica Le Scienze presenta un problema invitando i lettori a inviare le soluzioni che saranno pubblicate nel numero successivo e anche sul blog curato dai cosiddetti Rudi Matematici, i tre auotori che rispondono ai nomi di Rudy d’Alembert, Alice Riddle e Piotr Rezierovic Silverbrahms.

Il quesito del mese di marzo 2022 è centrato sulla geometria dei triangoli e può essere così riassunto:

All’interno di un triangolo, si sceglie un punto P arbitrario. Da questo si tracciano le perpendicolari ai tre lati del triangolo. I piedi delle perpendicolari individuano tre punti sui lati definendo un altro triangolo, dal quale si ripete la stessa costruzione dal punto P. Ci si ferma quando si ottiene un triangolo simile all’originale.
Dimostrare che questo è sempre possibile.

La soluzione che ho inviato è stata pubblicata come potete leggere andando alla pagina dei Rudi Matematici  (LINK).

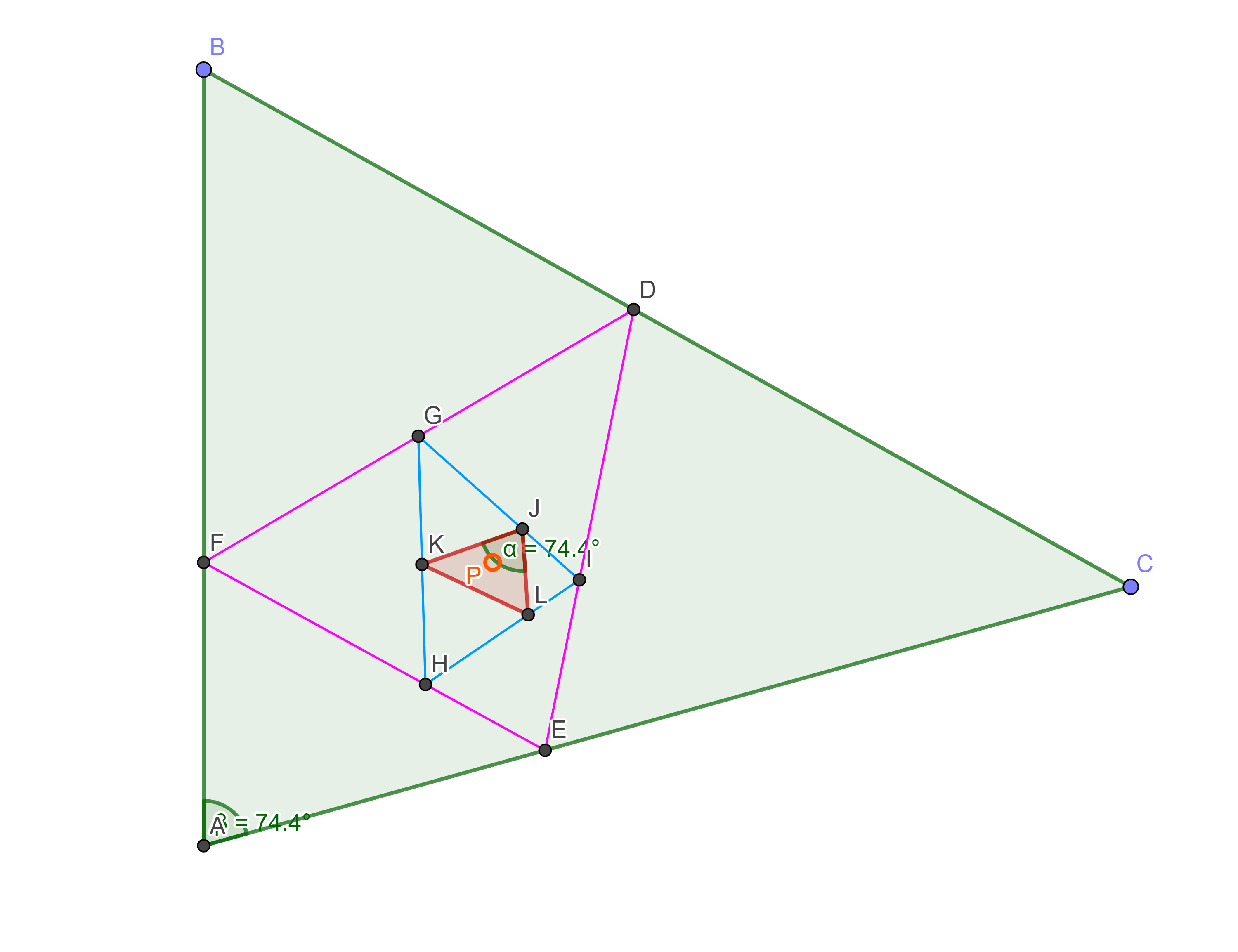
Sono diversi anni che le mie soluzioni sono pubblicate da Le Scienze e, diciamolo, riscuotono sempre un certo apprezzamento come potrete verificare visitando alcune delle pagine d’archivio a QUESTO LINK. Non compaiono tutte le mie soluzioni perchè, come in questo numero, i solutori vengono indicati col nome senza cognome (da tempo sono indicato solo come Giuseppe).

La soluzione completa potete leggerla in QUESTO pdf oppure direttamente dal sito di Le Scienze in cui è presente (l’unico caso!) il link con lo stesso file.

Perchè invio le soluzioni, esponendomi al rischio di qualche clamoroso “infortunio” che poi magari sarebbe pubblicato? Perchè la passione per la scienza e la matematica non cessano con la vita lavorativa ma continuano per sempre, almeno fino a quando si prova emozione nel misurarsi con le cose vere, quelle in cui non si decreta se si ha ragione per alzata di mano!

Il problema di «Le Scienze» pubblicato nel numero di Gennaio 2015 (vedi pagina) chiede di risolvere un interessante problema: come tagliare una fetta di torta di area massima con la condizione che sia ottenuta con un taglio simmetrico e con tre punti appartenenti alla circonferenza (raggi r, r e l’arco AB interno indicato con “a“) .

Schematizzando il problema con un disegno, ecco come si presenta la torta:
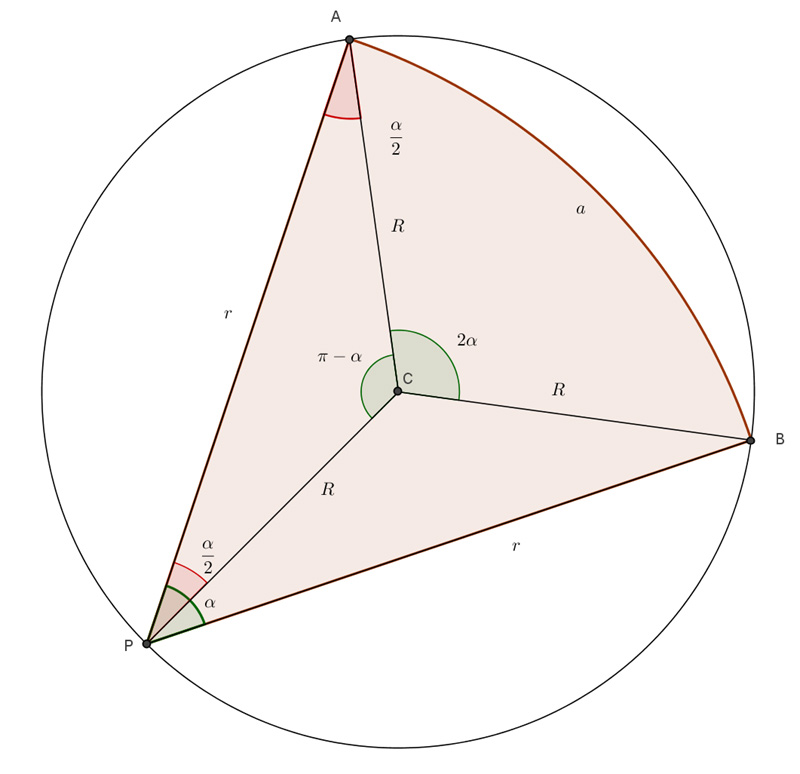Si tratta di un classico problema di massimo che si affronta trovando la funzione area e poi studiando la sua derivata.

La soluzione che ho trovato e che è molto piaciuta ai redattori della rivista, è

α= 1,3065423741888062022287278 radianti

oppure, espressa in gradi,

α= 74 gradi 51 primi e 33,70966567616054 secondi d’arco.

Tutti i passaggi sono presenti nella soluzione completa esposta nel pdf si può trovare qui. 

Qui di seguito inserisco i link per scaricare i file di Geogebra (estensione .ggb) che sono utili per studiare il problema e cercare la soluzione:

• da questo link si ottiene il file di Geogebra (con animazione) che illustra il problema;
• da questo link si può scaricare il file Geogebra che rappresenta la funzione S(α);
•  da questo si può scaricare il file che rappresenta l’andamento della derivata S'(α) per trovare graficamente i punti in cui si annulla (solo uno ci interessa).

I Rudi Matematici che hanno pubblicato la mia soluzione all’interno del blog che ogni mese dà le soluzioni pervenute, così commentano:

E l’abbiamo già detto, non riusciamo davvero a citare tutti i solutori (rischiamo perfino di confonderli… ad esempio, abbiamo più di un Lucio C. ….) ma non possiamo chiudere prima di salutare Giuseppe M., che ci scrive da un paese in Calabria che ha un nome delizioso e caratteristico, e che risolve virtualmente ogni nostro quesito. La soluzione di Giuseppe è molto bella, con grafici belli anche solo da guardare dal punto di vista estetico. L’abbiamo messa in un pdf, e potete trovarla qui.

A loro va il mio sentito ringraziamento per il commento e l’apprezzamento per la soluzione e anche perchè hanno sottolineato il dolce suono del nome della nostra amata Decollatura.

Problema di Le Scienze Settembre 2013: «Sarah Connor?»

Il problema ha un’enunciazione semplicissima:

Dato un giardino a forma di triangolo rettangolo (cateti 300 e 400 metri), trovare la siepe più breve per separarlo in due parti di area uguale.

Il contesto non appare molto complicato. Il fatto che si tratti di un triangolo con i lati che formano una terna pitagorica semplifica i calcoli ma non sarebbe stato essenziale.

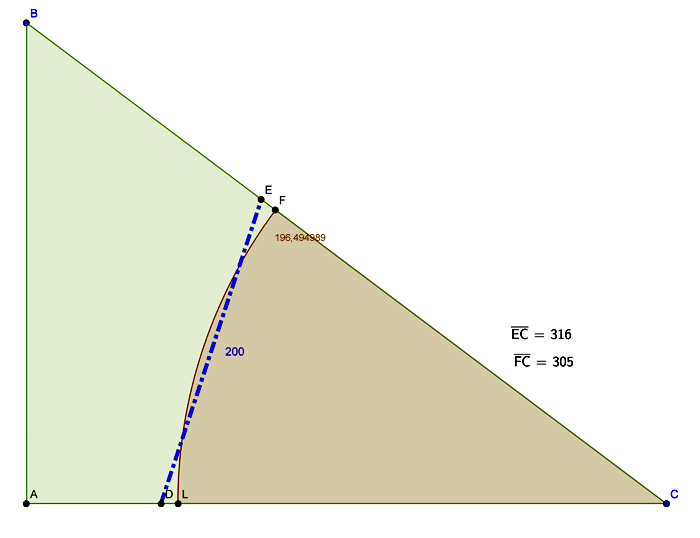
La siepe che divide in due parti uguali un giardino a forma di triangolo

Fissate i nomi dei vertici come in figura abbiamo che:

1. La lunghezza minima della siepe che divide in due il giardino è di 196,494989 metri. Si tratta di un arco di circonferenza con centro nel vertice in cui si uniscono l’ipotenusa e il cateto di 400 m, quindi quello che è il vertice dell’angolo minore, e avente raggio di circa 305,352145 metri.
2. Se per qualche motivo non si è disposti a fare una siepe curva, rimane l’alternativa della siepe rettilinea che unisce il punto E sull’ipotenusa con un punto D sul cateto maggiore entrambi distanti 316,227766 dal vertice dell’angolo minore che nel disegno allegato ho indicato con C. In questo caso la distanza è di 200 metri.

Dimostrazioni.

Punto A)

Costruiamo il settore circolare di centro C e angolo α dato da arcsen(3/5) circa uguale a 0,6435 radianti. Per avere un’area di 30000 metri quadrati (la metà dei 60000 metri quadrati dell’intero giardino) occorre un raggio r fornito dalla formula inversa dell’area del settore circolare. Da qui il valore proposto di 305,352145 metri.

Una volta noto il raggio, la lunghezza dell’arco si ottiene dalla definizione di misura in radianti di un angolo, per cui arco= raggio * angolo

quindi arco = 305,352145 * 0,6435 = 196,494989 metri

Punto B)

L’area di un triangolo si ottiene dalla nota formula trigonometrica secondo cui bisogna moltiplicare due lati qualsiasi per il seno dell’angolo tra essi compreso e dividere per due. Il seno dell’angolo è noto ed è 3/5 da cui, l’area è nota a priori ed è 30000 metri quadrati, da cui si deduce che i lati (uguali) sono lunghi 316,227766 m.

Trovati i due lati, ricaviamo il terzo (che è la lunghezza della siepe cercata) con la formula del coseno (o di Carnot) che ci dà appunto 200 metri esatti.

 OSSERVAZIONE

La scelta dell’altro angolo acuto, quello maggiore, come vertice del triangolo non sarebbe altrettanto valida poiché, essendo per angoli acuti il seno strettamente crescente e il coseno strettamente decrescente, la diminuzione del raggio necessario per avere una data area, sarebbe vanificata dalla piccolezza del contributo del coseno nella formula di Carnot nel non far aumentare il valore del lato opposto all’angolo scelto e che poi in definitiva è la lunghezza della siepe. Con l’altro angolo si otterrebbe una siepe curva di circa 236 metri.

Questa è la visualizzazione del problema con GeoGebra:

GeoGebra Foglio di lavoro dinamico

In questa seconda rappresentazione con GeoGebra si può osservare il comportamento della siepe se si sceglie un punto sull’ipotenusa (come nel primo caso) e il secondo punto sul cateto minore. In questo caso si osserva come la lunghezza della siepe non scenda mai sotto i 245 metri (circa):

GeoGebra Foglio di lavoro dinamico

Questo è il link alla pagina di Le Scienze con la soluzione al quesito.

Da qui e qui si possono prelevare i due file per GeoGebra per essere usati offline.

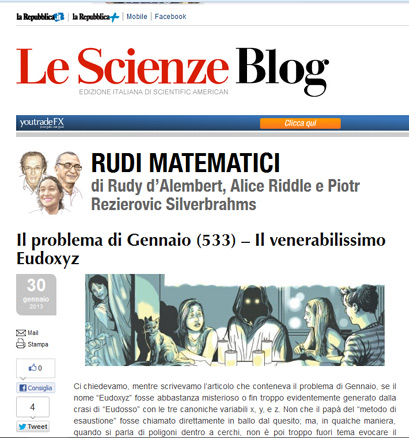
Il quesito di gennaio 2013 (533), intitolato  «Il venerabilissimo Eudoxyz» è così formulato:

Disegnare un pentagono concentrico con un cerchio di raggio dato in modo che i cinque rettangoli uguali aventi come uno dei lati il lato del pentagono e per l’altro lato il segmento perpendicolare al precedente e delimitato dalla circonferenza data, abbiano area massima.

La soluzione che ho proposto è la seguente:

Il pentagono che produrrà i cinque rettangoli di area massima è quello che ha come lato quello che avrebbe il decagono (regolare) inscritto in quella stessa circonferenza. Vale a dire che il suo lato sarà uguale alla sezione aurea del raggio del cerchio.

Ecco il disegno che rappresenta tutte le figure geometriche coinvolte:

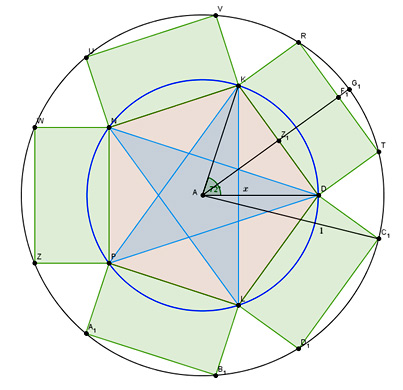
La dimostrazione completa è disponibile in questo pdf (cliccare sull’immagine che segue):

Da questo link si apre una nuova pagina html in cui è attiva l’applet di GeoGebra per vedere cosa succede quando si modifica la dimensione del pentagono interno.

Da quest’altro invece si apre una pagina simile alla precedente ma che contiene anche le misure dei segmenti e delle superfici. Inoltre, da un’apposita casella, si può inserire il valore del raggio del cerchio in cui è inscritto il pentagono richiesto per vedere il risultato.

Infine ecco le animazioni delle generalizzazioni: la prima per il triangolo/esagono (non interattiva) e la seconda per il caso del quadrato/ottagono (interattiva).

Questo è il link per la cartella zippata che contiene quattro file ggb per Geogebra che generano le figure che ho mostrato.

Ecco il link alla pagina del sito di Le Scienze che contiene il problema, le soluzioni e il blog:

GENERALIZZAZIONE DEL PROBLEMA

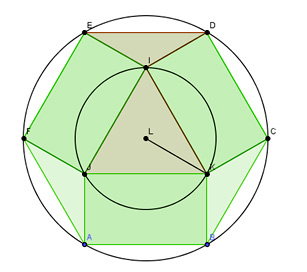
La proprietà sopra enunciata per il pentagono può essere generalizzata per tutti i poligoni nel seguente modo:

 l’area massima dei rettangoli costruiti sui lati  di un poligono regolare con n lati concentrico con un cerchio di raggio r, si ha quando il lato del poligono ha lunghezza pari a quello di 2n lati inscritto nel cerchio dato.

 Come conseguenza, ad esempio, il triangolo equilatero concentrico con il cerchio di raggio 1 per il quale i rettangoli costruiti sui lati hanno area massima, è il triangolo avente come lato quello dell’esagono regolare inscritto nel cerchio che, com’è noto, ha lunghezza 1.

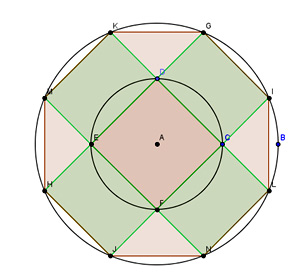
La stessa cosa accade con il quadrato, per il quale i rettangoli hanno l’area massima quando il lato su cui sono costruiti hanno lunghezza pari a quella dell’ottagono regolare  inscritto nella circonferenza. Se questa ha raggio 1 il valore del lato è 0,765366:

GENERALIZZAZIONE FINALE.

A questo punto, faccio la considerazione finale. Il lettore mi segua pazientemente.

Applichiamo la proprietà precedente — cioè la generalizzazione — in senso inverso. Si potrebbe enunciare così:

Il lato di un poligono regolare inscritto in una circonferenza di numero pari di lati (poniamo 2n) è uguale alla lunghezza dei lati di un poligono regolare di metà numero di lati e concentrico con il precedente, per il quale sia massima l’area dei rettangoli costruiti sui suoi n lati e delimitati dalla circonferenza.

Fin qui niente di strano. L’esagono produrrebbe un triangolo per il quale abbiamo già visto valere la proprietà, il dodecagono produrrebbe un esagono più piccolo e… e così via.
Proviamo però a considerare il quadrato come poligono di partenza, cioè quello con numero 2n di lati. Dal quadrato dovremmo ottenere un poligono con metà numero di lati e per il quale dovrebbe valere la stessa proprietà. Questo “poligono” avrebbe però… due lati!
Certo, lo sappiamo, è un poligono che non può esistere. Non c’è la fatidica spezzata che dovrebbe racchiudere una porzione di piano, ecc… .

Ma ammettiamo — per amore di ragionamento, si capisce — di concedere lo status di poligono a questo strano oggetto.

Potremmo anche farcene una ragione, immaginando di rimpicciolire sempre più il terzo lato di un triangolo (equilatero) fino a farlo sparire completamente, portando i vertici a diventare due, come quando si chiude un compasso. Non si può essere obbligati a dire che si ottiene un singolo segmento, potendo benissimo essere visto come due segmenti sovrapposti che, pur se costretti a occupare la stessa “sottile” posizione, sono pur sempre due segmenti distinti.
Uno va da A a B e l’altro va da B ad A. In fondo è lo stesso concetto dei due punti coincidenti che si adopera per definire la tangenza di retta e curva.

Ma torniamo al nostro aspirante poligono. Se fosse davvero tale dovrebbe condividere con gli altri la proprietà generalizzata che ho enunciato.
Per verificarlo usiamo lo stesso procedimento che si usa per passare dall’esagono (ad esempio) al triangolo. Cioè, prendendo il poligono con 2n lati – nel nostro caso il quadrato inscritto nella circonferenza – tracciamo le perpendicolari ai lati che sappiamo già essere i lati dei rettangoli e dei quali ci manca solo l’altezza.
I punti che saranno gli estremi dei lati del “poligono” piccolo li otteniamo dall’intersezione delle perpendicolari dei lati non consecutivi del quadrato (come d’altronde si deve fare per l’esagono).
Ora però accade che i lati non consecutivi del quadrato sono quelli che si trovano l’uno di fronte all’altro e le perpendicolari sono  coincidenti. Questo significa che il punto di intersezione non è determinato potendo essere uno qualunque, anzi tutti, i punti appartenenti agli altri due lati con il vincolo però della simmetria rispetto al centro. Prendiamo allora uno qualunque dei punti e, con la simmetria di cui sopra, anche il secondo.
Si ottiene la figura che segue in cui G e H sono i punti di cui si parla. I due rettangoli verdi, che al solito sono quelli richiesti dal problema, hanno area massima quando G e H corrispondono rispettivamente a M e N. In tale situazione la somma delle aree dei rettangoli uguagliano quella dell’intero quadrato originario e i “lati” del poligono sono uguali al lato del quadrato. Ecco la figura che si ottiene (da questo link si va all’animazione con GeoGebra):

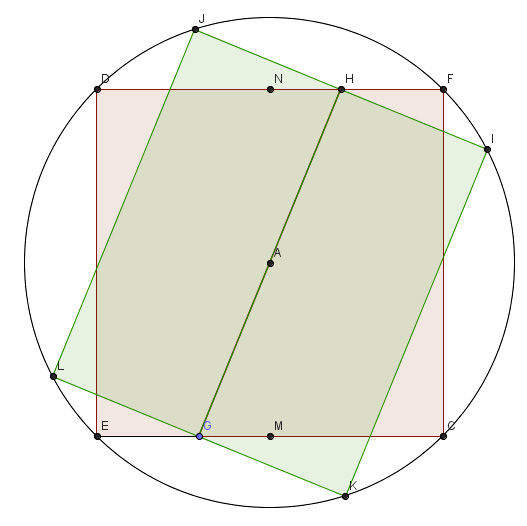
Il “poligono” con due lati, avrà superato il test per essere ammesso nel novero di questa nobile famiglia che di norma accetta solo membri con almeno tre lati?
Per essere chiuso in effetti il “poligono” è chiuso; la porzione di piano delimitata è definita, anche se è zero, che è pur sempre un signor numero. Inoltre, secondo la definizione, deve essere definito convesso poiché tutti i punti del segmento che congiunge due qualsiasi suoi punti appartengono al “poligono”.

Ai posteri l’ardua sentenza!

 Post Post Scriptum.

Con il quadrato, poligono con 4 lati, si chiude la possibilità di tentare a ritroso la scoperta di nuovi poligoni. Al triangolo manca la condizione necessaria e cioè quella di avere un numero pari di lati… altrimenti…

Post Post Post Scriptum

Ma allora perché non provare anche con il “poligono” a due lati per vedere se riesce a generarne uno con un lato. In fondo si parte da un numero pari di lati e quindi la cosa sarebbe fattibile.

Io però declino l’incarico!

Il Problema di Luglio 2008 (n. 479) – Dadi alla carbonara

Rudy propone ad Alice tre possibili giochi diversi, tutti basati sul lancio di tre dadi a 20 facce. Nel primo gioco, Rudy lancia due dadi, Alice lancia il terzo, e vince solo se il valore del suo dado è strettamente compreso tra i valori dei due dadi di Rudy. Nel secondo gioco, Rudy lancia due dadi, Alice ne sceglie uno dei due come proprio, e poi Rudy lancia il terzo per completare il gioco: le regole di vittoria per Alice sono le medesime del primo gioco. Infine, nel terzo gioco, Alice ha ancora un’opzione in più: dopo che Rudy ha lanciato i suoi primi due dadi, oltre a poter scegliere uno dei due come suo, Alice può anche decidere di lasciarli entrambi all’avversario e prendersi il terzo, quello che deve ancora essere lanciato. Quello che bisogna capire è se almeno uno dei tre giochi è favorevole ad Alice oppure no.

Qui potete trovare la mia soluzione che gli autori definiscono con queste parole «Una soluzione particolarmente bella ed estesa è arrivata da parte di Giuseppe Musolino: proprio per la sua estensione e per evitare di ridurla, cosa che sarebbe stata blasfema, la abbiamo riportata QUI. Secondo noi, si merita una lettura». Inutile aggiungere che la maggiore gratificazione viene da quei “blasfema” e “particolarmente bella“!

Clicca sull’immagine per andare alla pagina del sito di Le Scienze dedicata a questo problema e al blog dei solutori: