È stata pubblicata ieri 30 marzo la soluzione del problema I giardini di marzo. Ogni mese la prestigiosa rivista scientifica Le Scienze presenta un problema invitando i lettori a inviare le soluzioni che saranno pubblicate nel numero successivo e anche sul blog curato dai cosiddetti Rudi Matematici, i tre auotori che rispondono ai nomi di Rudy d’Alembert, Alice Riddle e Piotr Rezierovic Silverbrahms.

Il quesito del mese di marzo 2022 è centrato sulla geometria dei triangoli e può essere così riassunto:

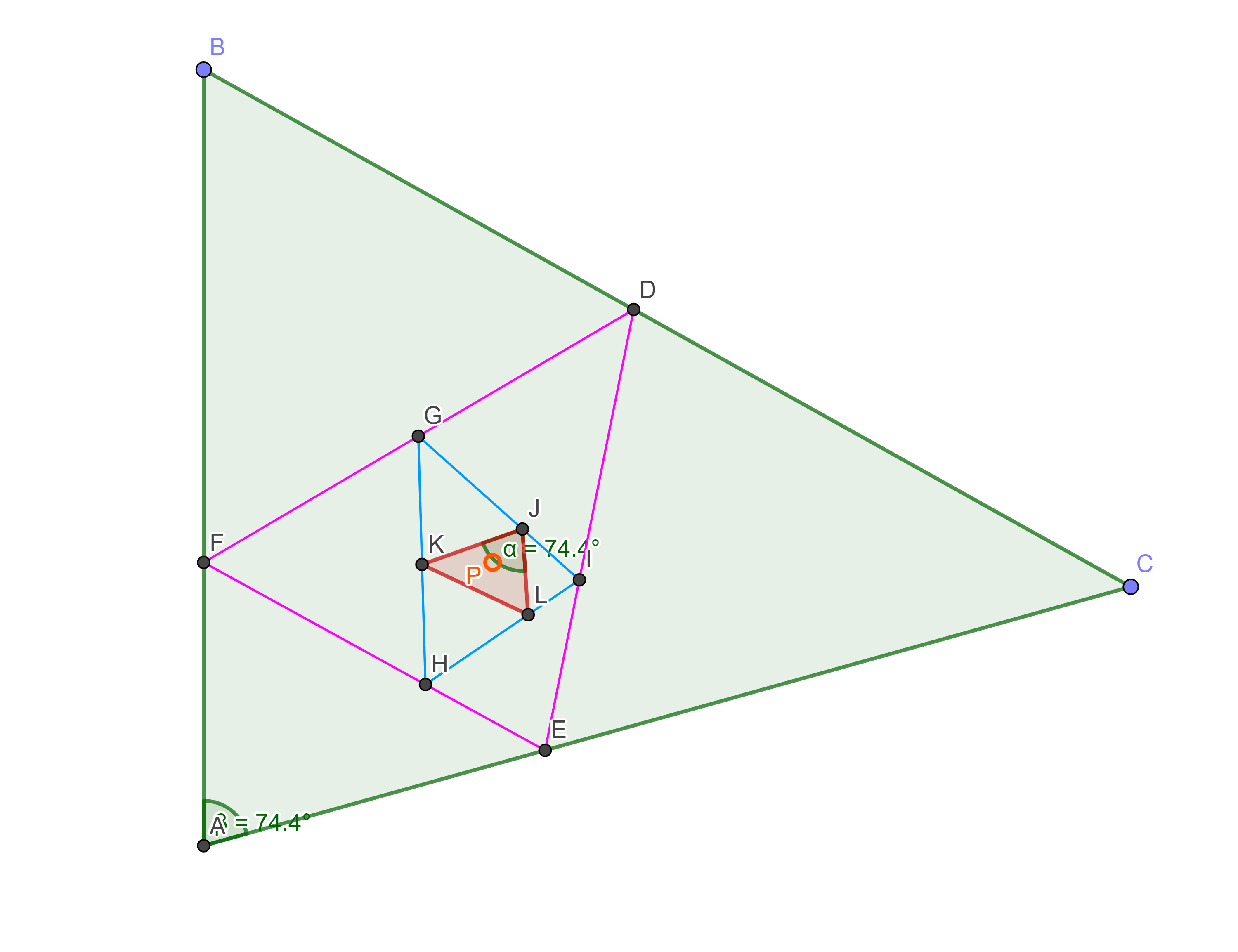
All’interno di un triangolo, si sceglie un punto P arbitrario. Da questo si tracciano le perpendicolari ai tre lati del triangolo. I piedi delle perpendicolari individuano tre punti sui lati definendo un altro triangolo, dal quale si ripete la stessa costruzione dal punto P. Ci si ferma quando si ottiene un triangolo simile all’originale.
Dimostrare che questo è sempre possibile.

La soluzione che ho inviato è stata pubblicata come potete leggere andando alla pagina dei Rudi Matematici  (LINK).

Sono diversi anni che le mie soluzioni sono pubblicate da Le Scienze e, diciamolo, riscuotono sempre un certo apprezzamento come potrete verificare visitando alcune delle pagine d’archivio a QUESTO LINK. Non compaiono tutte le mie soluzioni perchè, come in questo numero, i solutori vengono indicati col nome senza cognome (da tempo sono indicato solo come Giuseppe).

La soluzione completa potete leggerla in QUESTO pdf oppure direttamente dal sito di Le Scienze in cui è presente (l’unico caso!) il link con lo stesso file.

Perchè invio le soluzioni, esponendomi al rischio di qualche clamoroso “infortunio” che poi magari sarebbe pubblicato? Perchè la passione per la scienza e la matematica non cessano con la vita lavorativa ma continuano per sempre, almeno fino a quando si prova emozione nel misurarsi con le cose vere, quelle in cui non si decreta se si ha ragione per alzata di mano!

Il problema di febbraio 2015 ha come titolo “Tris triviale”.
Si tratta di una variante del gioco detto anche filetto. La particolarità consiste nel fatto che tutte le mosse di entrambi i giocatori avvengono in maniera casuale. In pratica è come se i giocatori nemmeno guardassero la scacchiera, persino quando la terza casella per fare il tris fosse libera e basterebbe occuparla con la propria pedina per vincere.

Nel tris normale si sa che il primo giocatore ha maggiori probabilità di vittoria, cioè si sa che con le sue mosse potrebbe imporre sempre il risultato di patta e potrebbe perdere solo dopo un grave errore.

Ma che succede nel tris casuale? Chi avrebbe maggiori probabilità di vincere? Questo è quanto chiede il problema del mese.

Il problema di «Le Scienze» pubblicato nel numero di Gennaio 2015 (vedi pagina) chiede di risolvere un interessante problema: come tagliare una fetta di torta di area massima con la condizione che sia ottenuta con un taglio simmetrico e con tre punti appartenenti alla circonferenza (raggi r, r e l’arco AB interno indicato con “a“) .

Schematizzando il problema con un disegno, ecco come si presenta la torta:
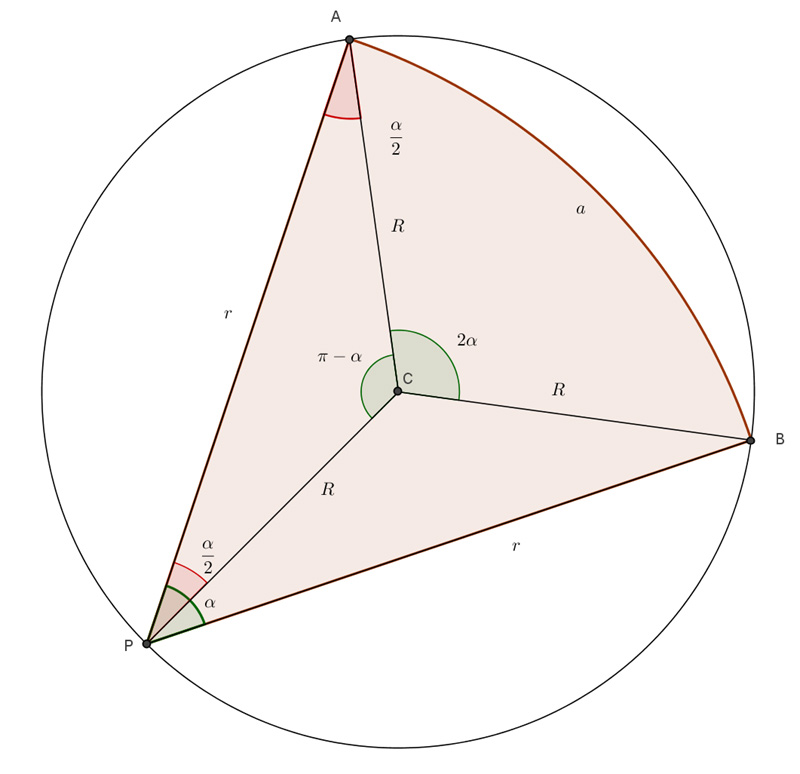Si tratta di un classico problema di massimo che si affronta trovando la funzione area e poi studiando la sua derivata.

La soluzione che ho trovato e che è molto piaciuta ai redattori della rivista, è

α= 1,3065423741888062022287278 radianti

oppure, espressa in gradi,

α= 74 gradi 51 primi e 33,70966567616054 secondi d’arco.

Tutti i passaggi sono presenti nella soluzione completa esposta nel pdf si può trovare qui. 

Qui di seguito inserisco i link per scaricare i file di Geogebra (estensione .ggb) che sono utili per studiare il problema e cercare la soluzione:

• da questo link si ottiene il file di Geogebra (con animazione) che illustra il problema;
• da questo link si può scaricare il file Geogebra che rappresenta la funzione S(α);
•  da questo si può scaricare il file che rappresenta l’andamento della derivata S'(α) per trovare graficamente i punti in cui si annulla (solo uno ci interessa).

I Rudi Matematici che hanno pubblicato la mia soluzione all’interno del blog che ogni mese dà le soluzioni pervenute, così commentano:

E l’abbiamo già detto, non riusciamo davvero a citare tutti i solutori (rischiamo perfino di confonderli… ad esempio, abbiamo più di un Lucio C. ….) ma non possiamo chiudere prima di salutare Giuseppe M., che ci scrive da un paese in Calabria che ha un nome delizioso e caratteristico, e che risolve virtualmente ogni nostro quesito. La soluzione di Giuseppe è molto bella, con grafici belli anche solo da guardare dal punto di vista estetico. L’abbiamo messa in un pdf, e potete trovarla qui.

A loro va il mio sentito ringraziamento per il commento e l’apprezzamento per la soluzione e anche perchè hanno sottolineato il dolce suono del nome della nostra amata Decollatura.