
Il problema di «Le Scienze» febbraio 2015 (558) “Tris triviale”
Scritto da Giuseppe Musolino il Mar 15, 2015 | 0 comments
Il problema di febbraio 2015 ha come titolo “Tris triviale”.
Si tratta di una variante del gioco detto anche filetto. La particolarità consiste nel fatto che tutte le mosse di entrambi i giocatori avvengono in maniera casuale. In pratica è come se i giocatori nemmeno guardassero la scacchiera, persino quando la terza casella per fare il tris fosse libera e basterebbe occuparla con la propria pedina per vincere.
Nel tris normale si sa che il primo giocatore ha maggiori probabilità di vittoria, cioè si sa che con le sue mosse potrebbe imporre sempre il risultato di patta e potrebbe perdere solo dopo un grave errore.
Ma che succede nel tris casuale? Chi avrebbe maggiori probabilità di vincere? Questo è quanto chiede il problema del mese.
L’approccio risolutivo può essere di due tipi. Uno è quello di calcolare la probabilià matematica dei tre eventi, vittoria giocatore che gioca per primo, vittoria del secondo giocatore e probabilità che la partita finisca patta.
Di queste tre probabilità bisogna calcolarne solo due dal momento che il totale deve dare il 100% e pertanto una delle tre probabilità può essere ricavata per differenza.
La probabilità matematica della vittoria del primo giocatore può essere calcolata dal rapporto tra il numero dei casi favorevoli e il numero dei casi possibili, analogamente alla vittoria del secondo giocatore. Ora, questo è il punto più difficile del problema poichè il calcolo dei casi favorevoli non è per niente semplice. Bisogna considerare il rischio di includere nel calcolo soluzioni duplicate e così via, insomma un percorso molto difficile basato sulla correttezza del modello seguito.
L’altro metodo che si può scegliere è quello della definzione frequentista di probabilità cioè quello di giocare effettivamente le partite e prendere nota dei risultati. Per la legge dei grandi numeri la frequenza dei tre esiti che ci interessano tenderà alla probabilità matematica e così si può ottenere una stima della probabilità. Se si dispone di un computer e di un adeguato software si può lasciare che sia lui a giocare migliaia di partite casuali e prendere nota dei risultati.
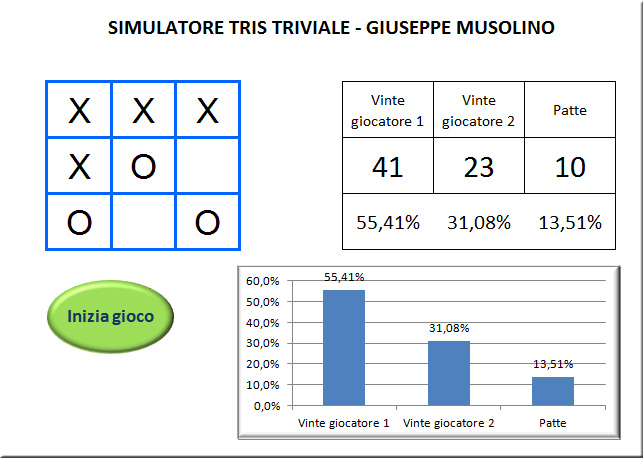
E’ quello che ho fatto utilizzando Excel nel file può essere scaricato cliccando sull’immagine:
I risultati che ho ottenuto sono i seguenti:
Frequenza vittorie giocatore 1 (quello che inizia indicato con la X): 57,79%
Frequenza vittorie giocatore 2 (quello che gioca per secondo indicato con la O): 28,70%
Frequenza partite patte: 13,51%
La statistica è stata condotta su circa 50000 partite, ottenendo qualche cambiamento non significativo anche con un maggior numero di prove.
Dal confronto con i risultati pubblicati sul blog di «Le Scienze» si può notare una differenza con quanto trovato da altri solutori. La maggior parte di questi però ha usato l’approccio della probabilità matematica, affrontando il calcolo davvero molto difficile delle combinazioni. Ad esempio Bruno ha trovato:
– Vince il primo giocatore: 58,49%
– Vince il secondo giocatore: 28,81%
– Partita patta: 12,70%
La differenza non è molta ma tuttavia è significativa per quanto riguarda il primo giocatore e le patte. Non conosco il motivo per cui si verifica ma è molto probabile che sia dovuto alle definizioni utilizzate nel calcolo.
Ad esempio, nella soluzione pubblicata sulla rivista (cartacea) di marzo dai Rudi Matematici, scopro che loro considerano “patta” la partita che si conclude con il tris fatto da entrambi i giocatori, dal momento che ipotizzano che comunque vada la partita le nove caselle della scacchiera siano sempre riempite. Questa però non è esattamente quella che si potrebbe dire una partita di tris poichè nel caso reale il gioco termina appena uno dei due giocatori allinea tre delle sue pedine.
Cercherò di discuterne sul blog.



Le ho inviato una e-mail