
Problema di Le Scienze Settembre 2013 «Sarah Connor?»
Scritto da Giuseppe Musolino il Set 30, 2013 | 0 commentsProblema di Le Scienze Settembre 2013: «Sarah Connor?»
Il problema ha un’enunciazione semplicissima:
Dato un giardino a forma di triangolo rettangolo (cateti 300 e 400 metri), trovare la siepe più breve per separarlo in due parti di area uguale.
Il contesto non appare molto complicato. Il fatto che si tratti di un triangolo con i lati che formano una terna pitagorica semplifica i calcoli ma non sarebbe stato essenziale.
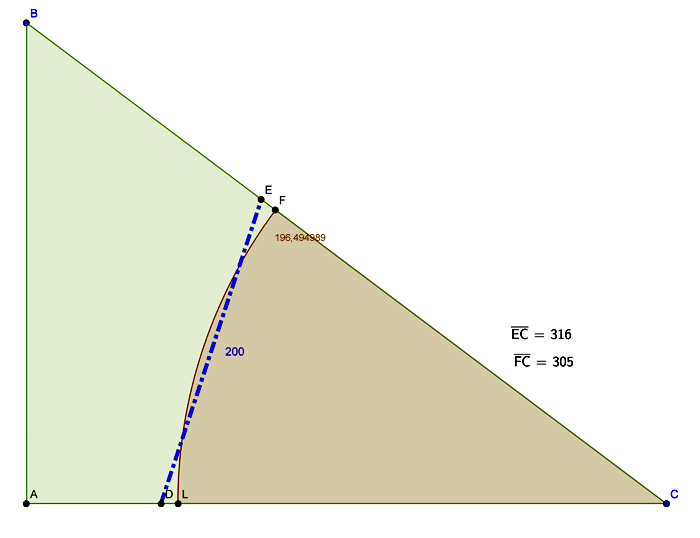
Fissate i nomi dei vertici come in figura abbiamo che:
- La lunghezza minima della siepe che divide in due il giardino è di 196,494989 metri. Si tratta di un arco di circonferenza con centro nel vertice in cui si uniscono l’ipotenusa e il cateto di 400 m, quindi quello che è il vertice dell’angolo minore, e avente raggio di circa 305,352145 metri.
- Se per qualche motivo non si è disposti a fare una siepe curva, rimane l’alternativa della siepe rettilinea che unisce il punto E sull’ipotenusa con un punto D sul cateto maggiore entrambi distanti 316,227766 dal vertice dell’angolo minore che nel disegno allegato ho indicato con C. In questo caso la distanza è di 200 metri.
Dimostrazioni.
Punto A)
Costruiamo il settore circolare di centro C e angolo α dato da arcsen(3/5) circa uguale a 0,6435 radianti. Per avere un’area di 30000 metri quadrati (la metà dei 60000 metri quadrati dell’intero giardino) occorre un raggio r fornito dalla formula inversa dell’area del settore circolare. Da qui il valore proposto di 305,352145 metri.
Una volta noto il raggio, la lunghezza dell’arco si ottiene dalla definizione di misura in radianti di un angolo, per cui arco= raggio * angolo
quindi arco = 305,352145 * 0,6435 = 196,494989 metri
Punto B)
L’area di un triangolo si ottiene dalla nota formula trigonometrica secondo cui bisogna moltiplicare due lati qualsiasi per il seno dell’angolo tra essi compreso e dividere per due. Il seno dell’angolo è noto ed è 3/5 da cui, l’area è nota a priori ed è 30000 metri quadrati, da cui si deduce che i lati (uguali) sono lunghi 316,227766 m.
Trovati i due lati, ricaviamo il terzo (che è la lunghezza della siepe cercata) con la formula del coseno (o di Carnot) che ci dà appunto 200 metri esatti.
OSSERVAZIONE
La scelta dell’altro angolo acuto, quello maggiore, come vertice del triangolo non sarebbe altrettanto valida poiché, essendo per angoli acuti il seno strettamente crescente e il coseno strettamente decrescente, la diminuzione del raggio necessario per avere una data area, sarebbe vanificata dalla piccolezza del contributo del coseno nella formula di Carnot nel non far aumentare il valore del lato opposto all’angolo scelto e che poi in definitiva è la lunghezza della siepe. Con l’altro angolo si otterrebbe una siepe curva di circa 236 metri.
Questa è la visualizzazione del problema con GeoGebra:
GeoGebra Foglio di lavoro dinamico
In questa seconda rappresentazione con GeoGebra si può osservare il comportamento della siepe se si sceglie un punto sull’ipotenusa (come nel primo caso) e il secondo punto sul cateto minore. In questo caso si osserva come la lunghezza della siepe non scenda mai sotto i 245 metri (circa):
GeoGebra Foglio di lavoro dinamico
Questo è il link alla pagina di Le Scienze con la soluzione al quesito.
Da qui e qui si possono prelevare i due file per GeoGebra per essere usati offline.


Le ho inviato una e-mail